SM4 国密算法

SM4 算法

[TOC]

代码实现 tzzs/GM (github.com)

1. 国密 SM4 算法

SM4 分组密码算法是我国自主设计的分组对称密码算法，用于实现数据的加密/解密，以保证数据和信息的机密性。其算法公开，分组长度与密钥长度均为 128bit，加密算法与密钥扩展算法都采用32 轮非线性迭代结构，S 盒为固定的 8 比特输入 8 比特输出。

2. 分组加密

分组加密（英语：Block cipher），又称分块加密或块密码，是一种对称密钥算法。分组加密（英语：Block cipher），又称分块加密或块密码，是一种对称密钥算法。例如： AES 3DES

3. S 盒

在密码学中，一个S 盒（Substitution-box，替换盒）是对称密钥加密算法执行替换计算的基本结构。在块密码（分组加密）中，它们通常用于模糊密钥与密文之间的关系——香农的混淆理论。

通常，S-Box 接受特定数量的输入比特m，并将其转换为特定数量的输出比特n，其中n 不一定等于m。

3.1 DES S-box

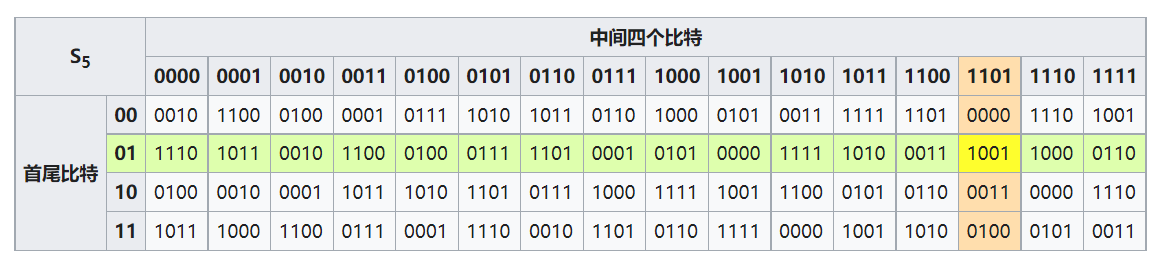
011011

100101

3.2 SM4 S-box

S 盒为固定的 8 比特输入 8 比特输出的置换

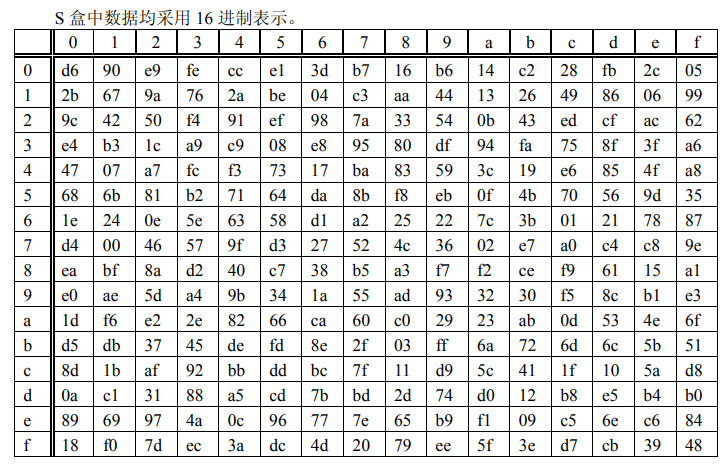
4. 加/解密方式

SM4 算法加/解密算法的结构相同，只是使用轮密钥相反，其中解密轮密钥是加密轮密钥的逆序。

4.1 原理

每组 128 bit（4 Byte） 按照以下方式进行加密

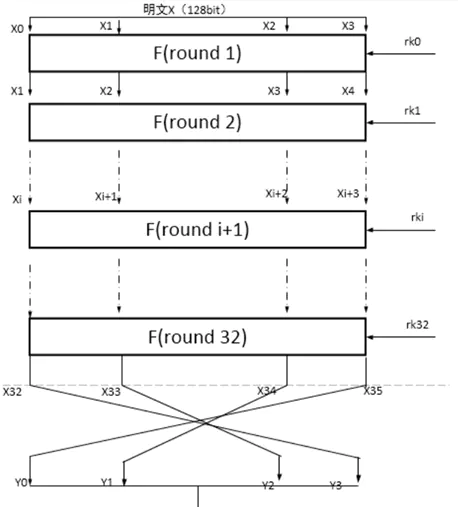
4.2 填充方式

将明文转化为字节，由于 SM4 加密算法按照 128 个位进行分组，最后一个分组不够 128 位的情况，需要进行填充（ZeroPadding、PKCS7Padding、PKCS5Padding)

• ZeroPadding

数据长度不对齐时使用0填充，否则不填充。

• PKCS7Padding

假设数据长度需要填充 n(n>0)个字节才对齐，那么填充 n 个字节，每个字节都是n;

如果数据本身就已经对齐了，则填充一块长度为块大小的数据，每个字节都是块大小。

// block size: 8 Btye / 64 bit

DD DD DD DD DD DD DD DD | DD DD DD DD
         8 Byte
DD DD DD DD DD DD DD DD |

• PKCS5Padding

PKCS7Padding 的子集，块大小固定为8字节。

4.3 参数

• 输入 X

  X0 X1 X2 X3 由 128 bit 拆分

• 加密密钥 MK, 128 bit

  MK=(MK0, MK1, MK2, MK3)

• 轮密钥 rk

  共计 32 轮，32 个轮密钥

• 轮函数 F

  每轮处理方式对应的函数

• 系统参数 FK, 4 个

  FK0=(A3B1BAC6)，FK1=(56AA3350)，FK2=(677D9197)，FK3=(B27022DC)

• 固定参数 CK, 32 个

  00070e15, 1c232a31, 383f464d, 545b6269,
  70777e85, 8c939aa1, a8afb6bd, c4cbd2d9,
  e0e7eef5, fc030a11, 181f262d, 343b4249,
  50575e65, 6c737a81, 888f969d, a4abb2b9,
  c0c7ced5, dce3eaf1, f8ff060d, 141b2229,
  30373e45, 4c535a61, 686f767d, 848b9299,
  a0a7aeb5, bcc3cad1, d8dfe6ed, f4fb0209,
  10171e25, 2c333a41, 484f565d, 646b7279

4.4 轮函数 F

$X_4 = F(X_0,X_1,X_2,X_3,rk) = X_0 \oplus T (X_1 \oplus X_2\oplus X_3\oplus rk_0)$

4.4.1 合成置换 T

一个可逆变换，由非线性变换 τ 和线性变换 L 复合而成,即 T(.)=L(τ(.))。

$T(A_0,A_1,A_2,A_3) = L(\tau(A_0,A_1,A_2,A_3))$

4.4.1.1 非线性变换

由 4 个并行的 S 盒构成

$B = \tau(A) = \tau(A_0,A_1,A_2,A_3) = (Sbox(A_0),Sbox(A_1),Sbox(A_2),Sbox(A_3))$

4.4.1.2 线性变换 L

非线性变换 τ 的输出是线性变换 L 的输入

$C = L(B) = B \oplus (B <<< 2) \oplus (B <<< 10) \oplus (B <<< 18) \oplus (B <<< 24)$

4.5 加/解密算法

明文输入：（X₀ , X₁, X₂, X₃）

密文输出： （Y₀ , Y₁, Y₂, Y₃）

轮密钥： rk_i (解密时为倒序)

$X_{i+4} = F(X_i,X_{i+1},X_{i+2},X_{i+3},rk) = X_i \oplus T (X_{i+1} \oplus X_{i+2}\oplus X_{i+3}\oplus rk)$

$(Y_0,Y_1,Y_2,Y_3) = R(X_{32},X_{33}, X_{34}, X_{35}) = (X_{35},X_{34}, X_{33}, X_{32})$

4.6 密钥扩展算法

本算法中加密算法的轮密钥由加密密钥通过密钥扩展算法生成。

$(K_0,K_1,K_2,K_3) = (MK_0 \oplus FK_0,MK_1 \oplus FK_1,MK_2 \oplus FK_2,MK_3 \oplus FK_3)$

---

$rk_i 轮密钥，i = 0,1,2,...,31$

$rk_i = K_{i+4} = K_i \oplus T'(K_{i+1} \oplus K_{i+2} \oplus K_{i+3} \oplus CK_i)$

---

$T'(B_0,B_1,B_2,B_3) = L'(\tau(B_0,B_1,B_2,B_3))$

$L’(B) = B\oplus (B<<<13) \oplus (B <<< 23)$